事実の共通項に着目する帰納法
帰納法(きのうほう)は、ロジカルシンキングを使ったコミュニケーションの際に使う考え方の一つで、「さまざまな情報の共通項を抽出する」ことによって論を構築する方法を指します。
たとえば、「アリストテレスは死んだ」、「プラトンも死んだ」、「ピタゴラスも死んだ」という三つの事実の共通項を抽出するならば、「人間は必ず死ぬ」という主張(結論)が導き出されます。
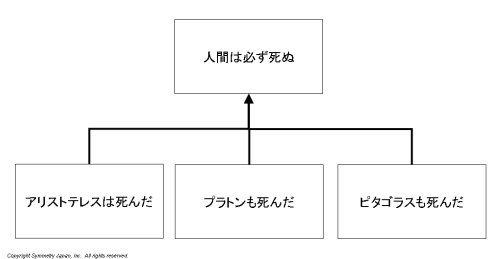
なお、帰納法とともに有名な論理展開の方法として、演繹法があり、主張と根拠をつなげて論を展開する際には、演繹法・帰納法のいずれかを使うことになります。
帰納法の三大チェックポイント
上記の通り帰納法は情報の間に共通する要素に注目しますが、そこから導き出される結論はひとつとは限りません。たとえば先ほどの「アリストテレスは死んだ」、「プラトンも死んだ」、「ピタゴラスも死んだ」という例は、「人間は必ず死ぬ」以外にも、
- ギリシャの賢人は必ず死ぬ
- カタカナの名前を持った人は必ず死ぬ
- 人間の中には死ぬ人もいる
なども、純粋にロジカルシンキングの観点からは主張として成立します。
ここに帰納法の難しさがあり、どの結論がもっとも確率が高そうか、を考えながら主張を導き出す必要があります。
このため、帰納法を使う際には、「帰納法の三大チェックポイント」で自分の導き出した主張の「たしからしさ」をチェックすることが大切です。
- 過度の一般化はないか
- ゆるい共通項はないか
- 因果関係のとり違いはないか
- 最後の藁の錯誤
- 因果の逆転
- 第三因子
帰納法の三大チェックポイント
| 前ページ 演繹法 (えんえきほう)を読む |
次ページ ポーターの5Fを読む |
|
|---|---|---|
| ロジカルシンキング研修のページに戻る | ||







